FONKSİYONLAR BİLEŞKE, BİLEŞKE FONKSİYONLARIN ÖZELLİKLERİ İLE İLGİLİ KONU ANLATIMLAR (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR)
Bileşke Kavramı
Bileşke fonksiyonuna, fonksiyon fonksiyonu da denir.
FONKSİYONLARIN BİLEŞKESİ
Tanım (FONKSİYONLARIN BİLEŞKESİ)
Örnek 1: 
 ve
ve 
 fonksiyonları için
fonksiyonları için 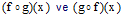 ve
ve  fonksiyonlarını bulunuz.
fonksiyonlarını bulunuz.
Yanıt 1:
Örnek 2: 
 ve
ve 
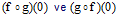 fonksiyonları için
fonksiyonları için 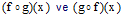 ve
ve  fonksiyonlarını bulunuz.
fonksiyonlarını bulunuz.
Yanıt 2:
Örnek 3: 
 ve
ve 
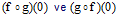 fonksiyonları için
fonksiyonları için 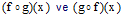 ve
ve  fonksiyonlarını bulunuz.
fonksiyonlarını bulunuz.
Yanıt 3:
Örnek 4: 
 ve
ve 
 fonksiyonları için
fonksiyonları için  ve
ve  fonksiyonlarını bulunuz.
fonksiyonlarını bulunuz.
Yanıt 4:
Örnek 5: 
 ve
ve 
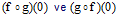 fonksiyonları için
fonksiyonları için  ve
ve  fonksiyonlarını bulunuz.
fonksiyonlarını bulunuz.
Yanıt 5:
Örnek 6: 
 ve
ve  için
için  bulunuz.
bulunuz.
Yanıt 6:
Bileşke fonksiyon bulunursa:
BİRİM (ÖZDEŞ-ETKİSİZ) FONKSİYON
Tanım (BİRİM (ÖZDEŞ-ETKİSİZ) FONKSİYON)
Örnek 1:  ve
ve 
 fonksiyonunun şemasını çiziniz.
fonksiyonunun şemasını çiziniz.
Yanıt 1:
Tanım ve görüntü kümeleri  dır. Tanım kümesi için gereken görüntü kümesinin elemanları:
dır. Tanım kümesi için gereken görüntü kümesinin elemanları:
 değerleri elde edilir.
değerleri elde edilir. Örnek 2: 
 fonksiyonunun birim fonksiyon olabilmesi için a, b ve c ne olmalıdır?
fonksiyonunun birim fonksiyon olabilmesi için a, b ve c ne olmalıdır?
Yanıt 2:
Örnek 3: 
 fonksiyonunun birim fonksiyon olabilmesi için a, b ve c ne olmalıdır?
fonksiyonunun birim fonksiyon olabilmesi için a, b ve c ne olmalıdır?
Yanıt 3:
FONKSİYONUN TERSİ
Tanım (FONKSİYONUN TERSİ)
Örnek 1: 
 fonksiyonunun tersini bulunuz.
fonksiyonunun tersini bulunuz.
Yanıt 1:
Fonksiyonun tersi  olarak alınırsa
olarak alınırsa  eşitliğinden yararlanırsak:
eşitliğinden yararlanırsak:
bulunur.
Örnek 2: 
 fonksiyonunun tersini bulunuz.
fonksiyonunun tersini bulunuz.
Yanıt 2:
Fonksiyonun tersi  olarak alınırsa
olarak alınırsa  eşitliğinden yararlanırsak:
eşitliğinden yararlanırsak:
bulunur.
Örnek 3: 
 fonksiyonunun tersini bulunuz.
fonksiyonunun tersini bulunuz.
Yanıt 3:
Fonksiyonun tersi  olarak alınırsa
olarak alınırsa  eşitliğinden yararlanırsak:
eşitliğinden yararlanırsak:
bulunur.
Örnek 4: 
 fonksiyonunun tersini bulunuz.
fonksiyonunun tersini bulunuz.
Yanıt 4:
Fonksiyonun tersi  olarak alınırsa
olarak alınırsa  eşitliğinden yararlanırsak:
eşitliğinden yararlanırsak:
bulunur.
Örnek 5: 
 fonksiyonunun tersini bulunuz.
fonksiyonunun tersini bulunuz.
Yanıt 5:
Fonksiyonun tersi  olarak alınırsa
olarak alınırsa  eşitliğinden yararlanırsak:
eşitliğinden yararlanırsak:
bulunur.
Örnek 6: 
 fonksiyonunun tersini bulunuz.
fonksiyonunun tersini bulunuz.
Yanıt 6:
Fonksiyonun tersi  olarak alınırsa
olarak alınırsa  eşitliğinden yararlanırsak:
eşitliğinden yararlanırsak:
bulunur.
Kural: 
 biçiminde verilen fonksiyonların tersi
biçiminde verilen fonksiyonların tersi  olur.
olur.
Örnek 7: 
 fonksiyonunun tersini bulunuz.
fonksiyonunun tersini bulunuz.
Yanıt 7:
Kural uygulanırsa f fonksiyonunun tersi  dir.
dir.
Örnek 8: 
 ise
ise  değerini bulunuz.
değerini bulunuz.
Yanıt 8:
Fonksiyonun tersi  olarak alınırsa
olarak alınırsa  eşitliğinden yararlanırsak:
eşitliğinden yararlanırsak:
bulunur.
Örnek 9: 
 ise
ise  değerini bulunuz.
değerini bulunuz.
Yanıt 9:
Kural uygulanırsa f fonksiyonunun tersi  dir.
dir.
bulunur.
BİLEŞKE FONKSİYONUN ÖZELİKLERİ
Bileşke fonksiyonunun özelikleri:
1. Değişme Özeliği
2. Birleşme Özeliği
3. Birim (Özdeş-Etkisiz) Fonksiyon Özeliği
4. Bileşke İçin  Özeliği
Özeliği
5. Bileşke İçin  Özeliği
Özeliği
6. Bileşke İçin  Özeliği
Özeliği
7. Bileşke İçin  Özeliği
Özeliği
8.
DEĞİŞME ÖZELİĞİ
Tanım (DEĞİŞME ÖZELİĞİ)
Örnek 1: 
 ve
ve 
 fonksiyonları için
fonksiyonları için  olduğunu gösteriniz.
olduğunu gösteriniz.
Yanıt 1:
Örnek 2: 
 ve
ve 
 fonksiyonları için
fonksiyonları için  olduğunu gösteriniz.
olduğunu gösteriniz.
Yanıt 2:
BİRLEŞME ÖZELİĞİ
Tanım (BİRLEŞME ÖZELİĞİ)
Örnek 1:  için
için 
 ve
ve  fonksiyonları için
fonksiyonları için
a)  fonksiyonlarını bulunuz.
fonksiyonlarını bulunuz.
b)  fonksiyonlarını bulunuz.
fonksiyonlarını bulunuz.
c)  değerini bulunuz.
değerini bulunuz.
Yanıt 1:
a) 
b) 
c) 
Sorunun a ve b parçalarına bakıldığında sonuçların eşit olduğu görülecektir. Böylece bileşke işleminin birleşme özeliği olduğu görülür.
Örnek 2:  için
için  olduğuna göre
olduğuna göre  değerini bulunuz.
değerini bulunuz.
Yanıt 2:
Örnek 3: 
 ve
ve  olduğuna göre
olduğuna göre  ve
ve  değerlerini bulunuz.
değerlerini bulunuz.
Yanıt 3:
Örnek 4: 
 ve
ve  için
için  bulunuz.
bulunuz.
Yanıt 4:
Bileşke fonksiyonu
Örnek 5: 
 ve
ve  için
için  bulunuz.
bulunuz.
Yanıt 5:
Bileşke fonksiyon bulunursa
BİRİM (ÖZDEŞ-ETKİSİZ) FONKSİYON ÖZELİĞİ
Tanım (BİRİM (ÖZDEŞ-ETKİSİZ) FONKSİYON ÖZELİĞİ)
Örnek 1:  fonksiyonunun birim fonksiyon olabilmesi için d, e ve f ne olmalıdır?
fonksiyonunun birim fonksiyon olabilmesi için d, e ve f ne olmalıdır?
Yanıt 1:
Birim fonksiyon  yani
yani  olduğundan
olduğundan
Örnek 2: 
 ise
ise  nedir?
nedir?
Yanıt 2:
Bileşke fonksiyon
BİLEŞKE İÇİN  ÖZELİĞİ
ÖZELİĞİ
Tanım ( ÖZELİĞİ)
ÖZELİĞİ)
Örnek 1: 
 için
için  değerini bulunuz.
değerini bulunuz.
Yanıt 1:
Bileşke fonksiyon  ve bundan
ve bundan  değeri hesaplanırsa
değeri hesaplanırsa
Örnek 2: 
 için
için  ve
ve  bulunuz.
bulunuz.
Yanıt 2:
Bileşke fonksiyonlar  ve
ve  bulunursa
bulunursa
BİLEŞKE İÇİN  ÖZELİĞİ
ÖZELİĞİ
Tanım ( ÖZELİĞİ)
ÖZELİĞİ)
Örnek 1: 
 için
için  bulunuz.
bulunuz.
Yanıt 1:
İlk önce  , sonra da
, sonra da  bulunursa:
bulunursa:
Örnek 2: 
 için
için  bulunuz.
bulunuz.
Yanıt 2:
İlk önce  , sonra da
, sonra da  bulunursa:
bulunursa:
BİLEŞKE İÇİN  ÖZELİĞİ
ÖZELİĞİ
Tanım ( ÖZELİĞİ)
ÖZELİĞİ)
Örnek 1: 

 için
için  bulunuz.
bulunuz.
Yanıt 1:
Buradan  bulunur.
bulunur.
Örnek 2: 

 için
için  bulunuz.
bulunuz.
Yanıt 2:
BİLEŞKE İÇİN  ÖZELİĞİ
ÖZELİĞİ
Tanım ( ÖZELİĞİ)
ÖZELİĞİ)
Örnek 1: 
 ise
ise  ve
ve  bulunuz.
bulunuz.
Yanıt 1:
Hiç yorum yok:
Yorum Gönder